En un sistema de coordenadas geográficas (GCS) se utiliza una superficie esférica de tres dimensiones para definir ubicaciones en la Tierra. Con frecuencia, a los GCS, Geographic Coordinate System (sistema de coordenadas geográficas) se los llama incorrectamente datum, pero un datum es solo una parte de un GCS. Un GCS incluye una unidad angular de medida, un meridiano base y un datum (basado en un esferoide).
Para hacer referencia a un punto se utilizan sus valores de latitud y longitud. La longitud y la latitud son ángulos medidos desde el centro de la Tierra hasta un punto de la superficie de la Tierra. Los ángulos se suelen medir en grados (o en grados centesimales). En la siguiente ilustración se muestra el mundo como un globo con valores de longitud y latitud.
En el sistema esférico, las líneas horizontales o líneas este-oeste son líneas de igual latitud, o paralelos. Las líneas verticales o líneas norte-sur son líneas de igual longitud, o meridianos. Estas líneas abarcan el globo y forman una red cuadriculada llamada retícula.
La línea de latitud que se encuentra en el punto medio entre los polos se denomina ecuador. Define la línea de latitud cero. La línea de longitud cero se denomina meridiano base. Para la mayoría de los sistemas de coordenadas geográficas, el meridiano base es la longitud que atraviesa Greenwich, Inglaterra. Otros países utilizan líneas de longitud que pasan a través de Berna, Bogotá y París como meridianos base. El origen de la retícula (0,0) se define por el punto donde se intersecan el ecuador y el meridiano base. El globo se divide, entonces, en cuatro cuadrantes geográficos basados en rumbos de brújula desde el origen. El norte y el sur están encima y debajo del ecuador, y el oeste y el este están a la izquierda y a la derecha del meridiano base.
 |
En esta ilustración se muestran los paralelos y los meridianos que forman una retícula.
|
Los valores de latitud y longitud se miden tradicionalmente en grados decimales o en grados, minutos y segundos (DMS, Degrees, Minutes and Seconds). Los valores de latitud se miden respecto al ecuador y van desde -90° en el polo sur hasta +90° en el polo norte. Los valores de longitud se miden respecto al meridiano base. Van de -180° cuando se viaja hacia el oeste hasta 180° cuando se viaja hacia el este. Si el meridiano base está en Greenwich, Australia, que está al sur del ecuador y al este de Greenwich, tiene valores de longitud positivos y valores de latitud negativos.
Puede ser útil igualar los valores de longitud con X y los valores de latitud con Y. Los datos definidos en un sistema de coordenadas geográficas se muestran como si un grado fuera una unidad lineal de medida. Este método es básicamente igual que la proyección de Plate Carrée.
Si bien la latitud y la longitud se pueden ubicar en posiciones exactas de la superficie del globo, no son unidades de medición uniformes. Solo a lo largo del ecuador la distancia que representa un grado de longitud se aproxima a la distancia que representa un grado de latitud. La razón es que el ecuador es la única línea paralela que es tan extensa como el meridiano. (Los círculos con el mismo radio que la Tierra esférica se denominan círculos grandes. El ecuador y todos los meridianos conforman círculos grandes).
Por encima y por debajo del ecuador, los círculos que definen las líneas paralelas de latitud se vuelven gradualmente más pequeñas hasta que se convierten en un solo punto en los polos norte y sur donde convergen los meridianos. A medida que los meridianos convergen hacia los polos, la distancia que representa un grado de longitud se reduce a cero. En el esferoide Clarke 1866, un grado de longitud en el ecuador equivale a 111,321 km, mientras que a una latitud de 60° equivale solo a 55,802 km. Dado que los grados de latitud y longitud no poseen una longitud estándar, no se puede medir distancias o áreas en forma precisa o visualizar datos fácilmente en un mapa plano o una pantalla de PC.
Las tablas de los sistemas de coordenadas geográficas compatibles, datums, etc. están disponibles en el archivo geographic_coordinate_systems.pdf en la carpeta de documentación de ArcGIS.





 es el momento lineal
es el momento lineal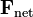 la fuerza total o
la fuerza total o 
 aplicando estas modificaciones a la ecuación anterior:
aplicando estas modificaciones a la ecuación anterior: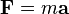
 y
y  . Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.
. Es decir la relación que hay entre la fuerza aplicada al cuerpo y la aceleración obtenida. Cuando un cuerpo tiene una gran resistencia a cambiar su aceleración (una gran masa) se dice que tiene mucha inercia. Es por esta razón por la que la masa se define como una medida de la inercia del cuerpo.
 a una
a una  (formado mediante el
(formado mediante el  perteneciente a un espacio
perteneciente a un espacio  , donde
, donde 
 ó bidimensional
ó bidimensional  ).
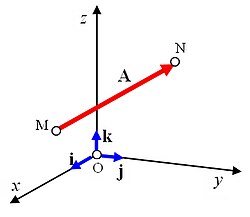
). , que indican su origen y extremo respectivamente.
, que indican su origen y extremo respectivamente.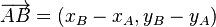
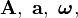 ... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector:
... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector:  ...
...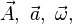 ... para los vectores y
... para los vectores y  ... o
... o 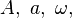 ... para los módulos.
... para los módulos. , ... resultando muy útil esta notación para los vectores que representan el desplazamiento.
, ... resultando muy útil esta notación para los vectores que representan el desplazamiento.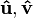 .
.
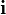 ,
,  ,
, 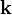 , paralelos a los ejes de coordenadas x, y, z positivos. Las componentes del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:
, paralelos a los ejes de coordenadas x, y, z positivos. Las componentes del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:

![\mathbf{a} = \begin{bmatrix}
a_x\\
a_y\\
a_z\\
\end{bmatrix}
\qquad
\mathbf{a} = [ a_x\ a_y\ a_z ]](http://upload.wikimedia.org/math/c/0/2/c02407847783cfc5ef04e2c0adbbb3d6.png)